窒化アルミニウム(AlN)は圧電薄膜共振器などに実用化されている圧電材料です。その材料特性の向上を目指した研究開発が進められており、AlをScで置換する、もしくは、MgとNbを同時に添加することにより、圧電定数が増大することが見出されています。Sc置換したAlNの圧電定数の第一原理計算による電子状態解析はすでに報告されていますので、私たちはMgとNbを同時添加したAlNの圧電定数を解析しました。

MgとNbを添加したAlNの原子配置
(仮想結晶近似)
AlNの単位格子は4原子から構成されており、この2x2x2スーパーセルを用意しました(計32原子)。絶縁性を保つためにMgとNbの比率を2:1にして、Mg 6個とNb 3個をそれぞれAlと置換すれば総置換率は56.3%です。ここで、MgとAlは周期表で並んだ元素であることに着目して、仮想結晶近似を用います。MgとAl各6個の代わりに、MgとAlの中間の性質を持つ”原子”(原子番号12.5)を12個用いて、その他Nbが3個、純粋なAlが1個、Nが16個から成る系を考えます(Mg6Nb3Al7N16)。3個のNbについて様々な配置を考慮することが望ましいですが、できるだけ均一に分布させた右の構造を原子配置の代表として採用しました。黄緑球がMgとAlの中間の性質を持つ”原子”です。 同様の考えに基づいて、Mg2Nb1Al5N8(置換率37.5%)とMg10Nb5Al9N24(同62.5%)も作成しました。
各置換率での原子配置を一つに限定するとともに、原子配置を均一にしたことにより系の対称性が高くなったことも利用して、計算量を少なく抑えました。圧電定数の第一原理計算は原子数に比して計算量が多いので、計算量削減は実用上重要です。

圧電定数の置換率依存性
このようにして求めた圧電定数の置換率依存性を示します。置換率62.5%で圧電歪定数d33は21.2 pC/Nとなり、純粋なAlNと比較して4.3倍に増大しました。この結果は、実験とよく合っています。圧電歪定数増大への最も大きな寄与は弾性定数C33の減少(約6割減)であり、次いで圧電応力定数e33の増大(最大4割増)であることが分かりました。
その他、格子定数の置換率依存性も実験結果を精度よく再現しています。詳しくは資料をダウンロードしてご覧ください。
資料ダウンロード
量子力学にしたがって物質の電子状態を計算するソフトウェア「PHASE/0」による解析事例紹介です。
解析対象: 圧電定数 / ボルン有効電荷 / 弾性定数
解析事例
「窒化アルミニウムの圧電定数」

エンタルピー差の圧力依存性
圧力(GPa) エンタルピー差:Hα - Hβ (eV)現在パワーデバイス材料の主流はシリコンであり、今後も当分その立場は揺るぎそうにありません。その一方で、エネルギー利用の高効率化を目指した次世代材料としてSiC, GaNの実用化・普及が着実に進展しています。そして「さらに次の世代」として酸化物エレクトロニクス材料Ga2O3が有望視されています。バンドギャップが大きいという基礎物性だけなく、高品質大型単結晶を安価に製造できることからその将来性に期待が持たれています。
Ga2O3には5つの結晶構造が知られていますが、主な研究対象はα型とβ型の二つです。常温常圧下での安定構造はβ型で、圧力を加えるとα型が安定になることが知られています(圧力誘起相転移)。第一原理バンド計算PHASE/0は圧力下での電子状態解析に対応していますので、この様子の再現を試みました。
α型、β型ともに圧力下での構造最適化計算を行って体積と内部エネルギーを求め、それらの値からエンタルピーを算出しました。両型のエンタルピー差の圧力依存性を左図に示します。約5 GPaでエンタルピー差の符号が反転し、安定構造が入れ替わることがわかります。相転移圧力の実験値には諸説ありますが(例えばJAP 107, 033520 (2010).)、その複数の結果と合うことを確認しました。

酸化ガリウムのラマンスペクトル
偏光ラマンの軸の向きは文献を参照;
α型,
β型
結晶構造が変化したことを検知する実験手法の一つがラマン分光です。ラマン分光は原子振動(フォノン)に伴う分極率変化を検出しますので、結晶構造毎に異なるフォノンの振る舞いがそのスペクトルに反映されます。そしてmatelier PHASE/0は一次の非共鳴ラマン分光の解析ができますので、実験結果との直接比較が可能です。
ラマンスペクトルの計算結果を右図に示します。PHASE/0 (GGA)の計算では、実験と比較して格子定数がわずかに大きくなる傾向があるため、フォノン振動数は小さめになる傾向があります。それを考慮すると、第一原理計算で求めたラマンスペクトルは、実験結果を再現しています。
資料ダウンロード
量子力学にしたがって物質の電子状態を計算するソフトウェア「PHASE/0」による解析事例紹介です。
解析対象: 圧力誘起相転移 / ラマン分光
解析事例
「酸化ガリウムの圧力誘起相転移とラマン分光」
半導体デバイス作製においては、結晶に含まれる不純物や欠陥が電子状態に及ぼす影響を理解し、制御することが重要です。このような電子状態解析は、第一原理バンド計算PHASE/0が最も得意とするところです。ここでは、パワーデバイス用材料として研究・開発が進められている窒化ガリウム(GaN)中の欠陥についてご紹介します。次に示す三種類の欠陥を考えます。

| 欠陥 | 生成エネルギー(eV) |
|---|---|
| VGa | 5.88 |
| VN | 3.46 |
| VGa-ON | 1.82 |
それぞれについて構造最適化を行い、欠陥の生成エネルギーを求めました。計算結果を表に示します。値が小さいほど、その欠陥が生じやすいことを意味します。この結果から、複合欠陥(VGa-ON)が最も生じやすいことがわかります。その電子状態をさらに詳しく調べます。
状態密度を下図左に示します。上向きスピンの状態密度(赤線)には、欠陥のないGaNのバンドギャップに対応する3eV程度のギャップがありますが、下向きスピンの状態密度(青線)には、ギャップ中に余分な準位が存在します。この準位の電荷密度分布を可視化しました(下図右)。欠損Gaと結合していたN原子上に局在していることがわかります。

状態密度図

電荷密度分布
資料ダウンロード
量子力学にしたがって物質の電子状態を計算するソフトウェア「PHASE/0」による解析事例紹介です。
解析対象: ワイドギャップ / 窒化ガリウム(GaN)中の欠陥
解析事例
「ワイドギャップ半導体中の欠陥準位解析」
鉄の高温安定相は非磁性の面心立方格子であり、比較的多くの他元素を固溶します。この固溶体はオーステナイトと呼ばれ、炭素原子であれば最大2.14重量%固溶することが知られています。それに比べると低温で安定なフェライト相(体心立方格子、強磁性)はほとんど炭素を固溶しません。そこで、炭素を多く含むオーステナイトを、炭素が拡散する時間を与えないように急冷すると、炭素を多く含む体心格子の鉄ができます(無拡散変態)。これがマルテンサイトであり、工業的に重要な材料です。その性質を第一原理バンド計算PHASE/0で解析しました。
最初に、マルテンサイト内での炭素原子の位置を調べました。炭素原子は侵入型(interstitial)で固溶していることが知られています。その原子位置の候補として四面体位置と八面体位置がありますので、それぞれに炭素原子を挿入した構造を作成し、どちらが安定かを調べます。系のサイズは、Bravais格子を3x3x3倍したスーパーセルに炭素原子を一つ挿入しました(全55原子)。そして構造最適化計算(格子定数の最適化を含む)の結果、炭素原子は八面体位置に侵入した方が安定であることが明らかになりました(0.89 eV/炭素原子)。それぞれの原子配置を図示します。左が八面体位置、右が四面体位置に炭素原子が侵入した場合です。 橙が鉄原子、灰色が炭素原子です。炭素原子とその最近接鉄原子を含む面内の電荷密度分布と併せて示します。

八面体位置

四面体位置

さてマルテンサイトでは、八面体位置に炭素原子が侵入した結果、一軸方向の歪を生じることが知られています。実際に先の構造最適化(格子定数の最適化)でも、c軸方向に格子が伸びる様子が確認できました。歪んだ格子の長さの比率は軸比と呼ばれ、磁気特性との関連が指摘されるなど、注目すべき物理量の一つです。そこで炭素濃度によって、どのように軸比が変化するのかを調べました。先の3x3x3スーパーセルに加えて2x2x2、4x4x4のスーパーセルを用意して、それぞれ一か所の八面体位置に炭素原子を配置し、構造最適化計算を行いました。軸比の計算結果を図に示します。軸比は炭素濃度に概ね比例することがわかります。

最後に、磁気モーメントを評価しました。鉄原子一つ当たりの磁気モーメントの大きさを図に示します。炭素濃度が高くなると軸比が増大するのは先に述べた通りですが、同時に磁気モーメントも大きくなる傾向が読み取れます。
これらの振る舞いは、実験および計算の文献値と良く一致しています(鉄と鋼, 100, 149 (2014).)。
資料ダウンロード
量子力学にしたがって物質の電子状態を計算するソフトウェア「PHASE/0」による解析事例紹介です。
解析対象: マルテンサイト / 軸比 / 磁気モーメント
解析事例
「鉄の軸比と磁気モーメントの解析」
 px, py
pz
s
px, py
pz
s
こちらで、グラフェンではπ電子が伝導を担っていることを電荷密度分布から見ましたので、ここでは原子軌道に射影した状態密度から確認します。右に示す計算結果から、px, py両軌道はs軌道と混成して結合性軌道(σ結合)を形成する一方、フェルミエネルギー近傍の電子状態はpz軌道(π結合)から成ることが読み取れます。

グラフェンナノリボン(zig-zag型)
赤青はスピン密度差を表す

バンド構造図
グラフェンのデバイス応用が期待されていますが、スイッチング素子に利用するにはバンドギャップを有することが望まれます。それを実現する方法の一つが「端」のある構造です。左図左のように両端を水素で終端した一次元構造(横方向に周期境界条件)はグラフェンナノリボン(zig-zag型)と呼ばれ、その電子状態解析ではスピン分極を考慮することが重要です。左図左の赤青は、上向き・下向きスピンの電子密度差を示しています。全体としては非磁性ですが、リボンの両端では逆向きにスピン偏極することにより系が安定化し、それに伴いバンドギャップを生じます(左図右)。
ギャップを形成する別の方法として、二層グラフェンに垂直に電場を印加することも検討されており、その電子状態解析も第一原理バンド計算PHASE/0で可能です。まず、電場を印加しない二層グラフェンを用意します(下図左)。この面間距離は、ファン・デル・ワールス相互作用(DFT-D2)を考慮して最適化しました。単層のグラフェンと同じように、この状態にはギャップがありません(下図中)。次にESM法を用いて、グラフェン垂直方向に0.2V/Åの電場を加えて電子状態を計算すると、バンドギャップが開きます(下図右)。

二層グラフェン
面間距離は3.23Å

状態密度図:電場なし

状態密度図:電場0.2V/Å

 ABA
ABC
ABA
ABC
単層、二層に続いて、三層グラフェンの電子状態にも特徴があります。三層グラフェンの原子配置(積層の仕方)は二種類あります。
 ABA
ABC
ABA
ABC
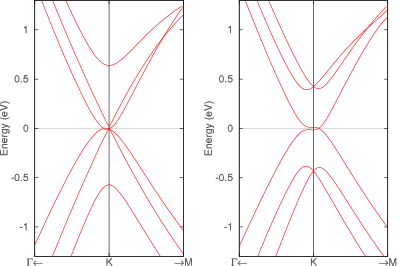
最安定原子配置はABAスタックですがABCも実在し、現在の技術ではこれらを作り分けることが可能です。そして両者のバンド構造には顕著な違いがあることが知られています。それぞれK点付近のバンド構造図を左に示します。ABAでは直線的なバンドがK点で交差してディラックコーンを形成するのに対して、ABCはK点にわずかなギャップがあり、ギャップが閉じるのはM点方向にずれたところです。さらに、これらに電場を印加するとABCスタックのみギャップを生じることも電子状態解析からわかっています。
資料ダウンロード
量子力学にしたがって物質の電子状態を計算するソフトウェア「PHASE/0」による解析事例紹介です。
解析対象: グラフェン / 射影状態密度 / 電場下の電子状態解析
解析事例
「グラフェンの電子状態解析」
「太陽光のエネルギーを用いて、水を酸素と水素に分解する。」
効率良く実行できれば、自然エネルギーへの転換に向けて大きく前進します。これを実現すべく、光触媒材料の研究が進められています。
光触媒材料はバンドギャップよりも高いエネルギー(短い波長)の光を吸収し、その際、電子-正孔対を生じます。そして、伝導帯下端(電子のエネルギー)が水素発生準位より高ければ(電位ではマイナス側)、水素が発生します。また、価電子帯上端(正孔のエネルギー)が酸素発生準位より低ければ(電位ではプラス側)、酸素が発生します。これらが同時に達成されると、水を酸素と水素に分解できます。

光触媒材料のエネルギー準位図
VBM:価電子帯上端、CBM:伝導帯下端、NHE:水素発生準位
水素発生準位に対する価電子帯上端と伝導帯下端の位置(すなわちバンドギャップも)を予測できれば、第一原理バンド計算は光触媒材料研究に貢献できます。バンドギャップを精度良く求めるためには、ハイブリッド汎関数を用いると良いでしょう。一方、第一原理バンド計算ではエネルギーの原点を決めることができず、価電子帯上端/伝導帯下端の水素発生準位に対する位置を求めることができません。この問題を解決するために、材料を構成する原子の性質(マリケン電気陰性度)のみを用いて、エネルギー原点を定める方法(Dalton Trans. 41, 11482 (2012).)が提案されています。この方法にしたがって計算した、各種材料のエネルギー準位図を示します。これらの結果は実験を概ね再現しており、第一原理バンド計算を光触媒材料探索に活用できることが分かります。
資料ダウンロード
量子力学にしたがって物質の電子状態を計算するソフトウェア「PHASE/0」による解析事例紹介です。
解析対象: バンドギャップ / ハイブリッド汎関数 / 光触媒材料
解析事例
「光触媒材料のバンドギャップ解析」
第一原理計算による受託解析を承っております。
電子状態を知りたい、物性値を予測したいなどのご要望、ご納期や費用、またお手元の課題にご対応可能かどうかにつきましても、ぜひ一度お問い合せください。